
gravity, light, time
Since the speed of light in every RF should always be measured the same, let us make a simple illustration: for RF layer which is two times faster (1 second of ours equals 2 seconds of faster RF layer) looking from our point of view, faster RF's speed of light should decrease two times. Otherwise, if speed of light stayed the same, in faster RF layer it would measure 299.792.458 meters per half a second (599.584.916 meters per second) which means, that the light speed in their RF would be two times faster. Since speed of light in that RF would also measure 299.792.458 meters per second, it means that meter unit - relatively to ours - would be two times smaller (it is going to be discussed in more detail later in this article).
Let us now go back to our spiral in fig. 2b. Since we presumed that speed of light is reversely proportional to time, for each RF that is slowing down we should accelerate speed of our light proportionally. And for faster RFs we will proportionally slow it down. The result of that operation is a curve shown in fig. 2c.
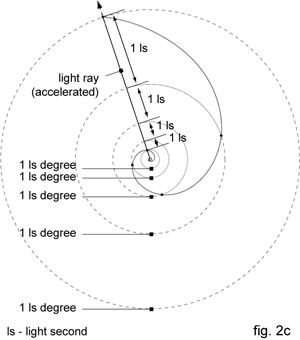
We are going to call it "the perception spiral". In the case of our light second clock - whichever RF we choose - our time perception would be one circle per time unit. Although we used different construction method, we got the exponential growth spiral from fig. 1.
The both spirals are degree sweep with radius of exponentially growing rotating square. So each distance from the centre has its square area aspect r2. Furthermore, the negative exponential growth equivalent of its square aspect would equal to 1/r2. Since gravitation is the force between bodies that is reversely proportional to the power of their distance its geometry curve would match spirals from figs.1 and 2c. Our perception spiral would be geometrical presentation of time - light speed - perception - gravitation connection.
Now we use our perception spiral to construct gravity clock. The orbit of our perception spiral with the value of 1 is going to be our rotation starting point which means that according to orbital growth direction we correspondingly switch our spiral rotation direction. The path between its centre and orbit-spiral intersecting point will be our g axis. The spiral is rotated in three different speeds. The first one turns twice faster and the last one twice slower than the middle one. The intersecting point between the g axis and the middle spiral will define the orbital distance, (l). The distance from rotation centre and the point at which faster spiral is cutting the g axis will make power of l. The distance between centre and slower spiral - g axis intersecting point would equal its root (fig. 3).
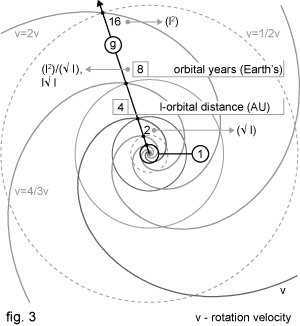
The result of dividing power of l with l root, is equal to Kepler's third law which explains speed of gravitational bodies orbiting around its centre at orbital distance l.
Second method multiplies our orbital distance with its root (twice slower rotating spiral).
For third method the spiral should be rotated one third faster. The distance between its intersecting point and centre of its rotation would give the orbital year’s value for one third slower rotating spiral (flesh application will come soon).
If orbiting speed of planet Earth (chosen as a RF for Solar system) is one year - which is one astronomic unit (1 AU) away from sun - the body on a distance of 4 AU would have the orbiting speed of 8 years. 16 AU would make 64, 64 would make 512 and 256 would be 4096 years. The body on a distance of 1024 AU would need 32768 years to close the circle and so on..
Imagine hand on our clock as a chord. For every 90 degrees of rotation in positive growth direction, our chord would vibrate two times slower and correspondingly it would play exactly one octave lower. To produce tones which get one octave higher we should make 90 degrees turns in negative growth direction. That makes each orbit producing a different sound. It was Kepler's idea explained in his work "Harmonies of the worlds", to apply different tones to planets orbiting in our solar system. According to that symphony of voices, Earth was condemned to eternally play "fa" and "mi" (relating to Latin word "fames" meaning "hunger", "greediness").
If our second hand chord would vibrate while rotating, we would suddenly hear very high sound appearing from silence, whose transformation would constantly accelerate towards lower sounds. At one moment, the sound would disappear. For some time, our instruments would still register vibration data although it would already be out of our direct perception range.
In accordance with our gravitational spiral, in lower gravity systems the chord would vibrate faster (distance between waves would shorten) than the chord in higher gravity systems. But imagine following vibrations by correspondingly changing gravity RF layers. The lower gravity would have faster time which means that the same number of waves would flow through one time unit. The same applies to higher gravity system chord. In other words, both scenarios would have the same frequency and we would always hear the same sound.
If our sound perception instruments located in ear grew or shrunk proportionally with our chord, we would constantly hear the same sound.
Now we will add three-dimensional value to our perception spiral by giving it speed of light input to its y axis. Each RF orbit should have corresponding speed of light, which means that two times slower time would have two times faster light and so on. The revolved cone resulting from a perception spiral rotating around y axis is going to be our spacetime "Absolute perception frustum"(fig.4a)
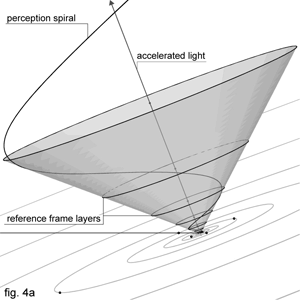
It is the 3D graphical presentation of our gravity - space - time diagram driven by absolute speed of perception whose measurable manifestation is speed of light (like a camera focal length without distortion).
Since each RF experienes the same time perception, and is measuring equal constant speed of light, we contract our "absolute perception frustum" y axis values to our RF speed of light. The result curved geometry of our gravity - spacetime cone will be our "relative perception frustum" (fig 4b.)
For each RF its shape would be the same.
Quantum mechanics and principle of relativity would explore events at its opposite edges..
The surface gravity on Earth is measured by its acceleration which is 9,807 m/s2. If we calculate Schwarzschild's formula for gravitational time dilation -
![]()
(Rs is a Schwarzschild's radius, Ro is radius, tf is nondilated and to is dilated time)
which was for our case
![]()
- we would get a result showing that one second in open space equals 1,0000000007 second on Earth’s surface. But what does one second in "open space" mean? Since gravity is endless, open space certainly cannot be attributed with zero gravity. If we calculate gravitational time dilation caused only by Sun’s gravity in Earth’s orbital distance one second would measure about 1,0000000097 seconds, which is more than gravitational time dilation on Earth's surface caused by Earth’s gravity. And what about gravitational influence of other bodies in our galaxy and other galaxies? If Earth is orbiting around the Sun and Sun is rotating around
The Big Bang theory we find in books is the consequence of relative observations of our RF measured with our speed of light.
While changing RF layers, which time should be calculated for gravitation? If Sun’s gravity in our RF was 274,187m/s2, measured from two times slower RF it would be 274,187 m/2s2 which is 137,0935 m/s2. From the sixty-fourth RF orbit of positive exponential growth, Sun’s gravity would be measured around 0,0000000000000000297m/s2 (2,97x10-17) and it would still have planets orbiting around it. Planet Earth would seem like an electron orbiting around its nucleus at a speed of about 292.304.368.285 orbital years per second. If speed of light didn't change, proportionally to that system it would have speed of about 2.765.097.373.977.159.828.519.256.064 meters per second. Even if it was much greater, measured from slower RF the result for Earth’s orbital speed would be about 0,99 parts of speed of light, since that would be the slower RF perception limit.
Considering the fact that light speed in Earth’s RF would decrease proportionally to its time unit increase - relative to slower RF in which we do our measurements - it would remain at speed of 299.792.458 m/s. There would be the same amount of waves passing through one distance unit in one second. It would mean that one meter would decrease 9.223.372.036.854.775.808 times, so the Sun’s gravity would remain at 274,187 m/s2. The mass and energy would decrease with light speed correspondingly. For the inside observer, Earth would still orbit around the Sun in a year time and it would take 24 hours to make a turn around its axis. Days, nights, seasons, light speed, mass and energy wouldn't change. All other relations inside Earth’s RF would stay the same. Looking from some beach in a bright summer night, the inner part of "primordial atom" substance wouldn’t look any different than our night sky...
There must be a place, from which our entire known universe looks like a tiny dot. Where its entire age and history lasts just a tiny fraction of a second. The convenient saying about universe being endlessly big is in fact more or less the same as a saying that it is endlessly small.
It appears as each local RF is built upon the percentage of the influence of gravitational bodies from its perception frustum range. Due to the fact, that its gravitational energy in our perception range is the most responsible for definition of our RF, the nucleus of our perception is the Sun. Correspondingly, orbiting electrons have most of their RF defined by their nucleus. Relatively to their perception layer other nucleuses are so far that it would take thousands of years to exchange signals with them. For their dimension layer, most of the objects that build our world are so red shifted that they literally don't exist. This principle allows hierarchical structure of different dimensions in universe. We might say that the borderlines of our RF perception frustum are quarks on one, and quasars on another side. To calculate gravity, speed of light, time and space relations for our layer, we choose Sun as our Solar system absolute RF. For this purpose, we would have to introduce solar units. Solar radius would be rs. Gravity on Sun’s surface (at 1 rs) would be 1 gs, which is one solar gravity. Time unit on 1 rs would have no dilation and it would be 1 ts (solar second). Speed of light at 1rs and 1ts would be one cs (solar speed of light). Since time and space contraction should be taken into consideration, dilated unit would be marked with d.
| solar units | |
| solar radius | rs |
| Gravity on Sun’s surface (at 1 rs) | gs |
| Time unit on 1 rs (no dilation) | ts |
| Speed of light at 1rs and 1ts | cs |
| dilated unit | d |
If we now expressed the gravity and speed of light change on different Sun radius units, we would get a following equation:
![]()
Since
![]()
in particular RF, we would get that
![]()
which is in fact an inverse square formula for gravitation with time dilation. Furthermore, it is
![]()
Calculating speed of light we get
![]()
and deriving from that we have
![]()
which again points to the fact that speed of light change equals to change of time (second) and space (meter). That is exactly what we did when constructing our perception spiral curve shown in fig. 2c.
To calculate Earth's gravitation (9,807 m/s2 by our conventions) in solar units, Earth rs would equal square root of Sun's gravity divided by Earth's gravity (273,96/9,807), where 273,96 m/s2 stands for a gravitation on the Sun’s surface, and it would count 5,28527470275608. That would be the solar radius distance from the sun, on which Sun’s gravity would be 9.807 m/s2. If we used a formula gs = cs/rs2d, by considering dilation between Sun's and Earth's surfaces, we would get 0,0357985 gs which equals a result we get dividing Earth's with Sun's gravity in conventional units.
If we measured one reference unit for mass of our RF in n times slower RF, in order to preserve mass-energy conservation between frames, its mass would be cut by cube function of n. The light speed, relatively to our frame would be scaled n times, so there would be only 1/n3 of its energy passing through its atom structure in one time unit of slower RF. That would make our RF meter n times shorter (fig. 6).
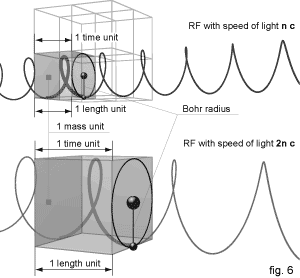
Calculated with our units, the planet in two times slower RF would have double diameter and eight times greater mass. But the real physical mass change would correspondingly change its particle structure mass. Furthermore, that change of electron and proton masses, would increase the length of Bohr radius with the consequence of slower orbital frequency. Its clock rate would slow down and its real length in more intense gravity field RF would increase. One meter would be longer and one kilogram would become heavier relatively to our RF. Since speed of light is driven by gravitation (c is actually a visible measurable aspect of g), famous equation
![]()
actually involves gravitation. For different RFs it would be
![]()
where td stands for time dilation. Relatively to other RF, our RF energy unit would change td times
![]()
Compared to more intense gravity fields our energy unit would decrease, which would lead to greater energy result expressed in our units. Since td for each particular system equals 1, we have
![]()
In other words, other RFs energy would change, relatively to our RF, by time dilation produced by its gravity
![]()
And since td = cd we can write the same equation as
![]()
More intense gravitational fields would increase the energy for their dilation amount and vice versa. This mass-energy preservation between frames can be applied in quantum mechanics, in both cases of size and time contraction due to kinetic energy and gravity.
Being somewhere on the edge of our galaxy and between its arms, means that part of our RF layer is defined with lower gravity than in
This is why the last point of the sixty-fourth arc of negative exponential growth spiral which appeared less than half a meter away from our eyes, was in fact 9,76 light years away, counted with units from that RF.
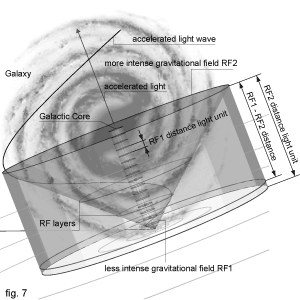
That might explain why galaxies don't obey inverse gravity rule while rotating, but rather act like a wheel. For what might appear to us as thousands of light years, for galaxy centre RF might be just "within reach of its arms". Therefore, the whole galaxy would behave like one body.
It is also consistent with the observation results that the biggest galaxies appear the furthest, with correspondingly greater red shift. That led to a conclusion that they are all running away from us with their speed increasing towards the edge of our observed universe. It is in fact their immense gravitation which puts them on the different scale of the edge of our perception range. The wavelength interpretation comes from the presumption of constant speed of light. If celestial body with its RF speed of light two times faster relative to ours, would move towards us, with its speed close to our RF speed of light, observed from our RF it would still be red shifted, and we would conclude that it is getting away from us. As the approaching galaxy would be getting closer, it would change our RF and our perception (with corresponding delay). Some blue shifted objects would disappear from our night sky, and some object we haven’t seen before would appear red shifted. Today’s known quasars would no longer be the furthest observed objects in our universe. The paintings of huge galaxies covering the night skies at some distanced planet horizons, which we might find in books, are in fact scenes that would be impossible to experience from any part of the universe. No matter how close we approach, we would never see the glow of the "shiny twirl" of the centre of our galaxy. Where ever we are and in which ever RF, the picture of universe would be very similar to ours. As we know, this idea was in fact first proposed in 16th century by Dominican priest Giordano Bruno who was burned for his heresy. It is quite obvious why the Big Bang theory with its creation act is so well accepted compromise for the Ptolemy’s model of the universe with Earth in centre of all things.
It is convenient to say that watching distanced galaxies is in fact observing some event that happened thousands or even billions of years ago. Those tiny dots, mostly visible only with a telescope have a diameter of hundreds of thousands light years. If we spotted supernova in the right part of that dot, it would take few hundred thousands of years to see the left part knowing about it. At the same time, some stars closer to the centre of a galaxy would know about it very short after the event took place. For some of their neighbours further towards centre, the event would be so blue shifted that they would never now about it. Other planets, in some dark regions between its arms, the whole area of a galaxy in which supernova took place might observe with a red shift so big, that they might know about supernova event ages after us. Or never know it at all. The clocks in different regions of that hardly visible dot would be so different that for some, the event would last a fraction of a second, while other regions might observe the cloud slowly spreading for millions of years (fig. 8).
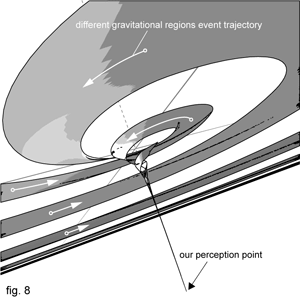
What creates such an unimaginable scenario happening in one hardly visible dot lost between billions of others somewhere on our night sky?
If we think of that force, which is endless, eternal, invisible, in destroyable and directly inmeasurable; the force which creates time, space and perception and the force that keeps universe together, the answer would most probably be close to religious. And the answer would be - Gravitation. In fact, since gravitation is endless, it is the irrefutable proof of the endlessness of universe with no beginning and no end. Where there is gravitation, there is time and space…
Einstein's general theory claims that, as a photon fights its way out of a gravitational field, it loses energy and its colour reddens. In fact, gravitational field is its energy source and - in the case of stars - its creator. It accelerates light with the consequence, in order to preserve perception, of time dilation. Thus, different RF layers are created.
Let us imagine light waves as a helix (conventional waves are its 2D presentation). Light travels in x axis direction. Each RF will be defined by the radius of a helix, which size is defined by y and z axes. Approaching gravitational field, helix proportionally grows in all three axes and shrinks the same way when moving away from it (it might be a good illustration for Bohr radius change). Bigger helix, in more intense gravitational fields, scaled by y and z axes to our RF radius would be registered as longer wavelength shifts. Correspondingly, yz scaled aspect of smaller helixes would fill our RF helix with shorter wavelengths shifts (fig. 9).
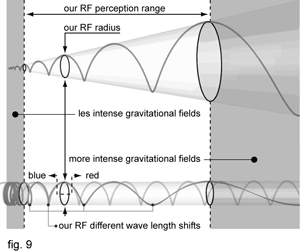
Instead of jumping, RF layers smoothly transform from one to another. The speed of light is in fact the speed of perception of each reference layer, and it is always measured the same. Scaled to our perception RF, shared regions between RFs are registered as different frequency shifts. If we travelled to lower gravity RF layer - measured from Earth (our start point) - we would become more and more blue shifted and observer on Earth would conclude that we are slowing down (a good example is a Pioneer anomaly which is going to be explained later in the text) (fig.10).
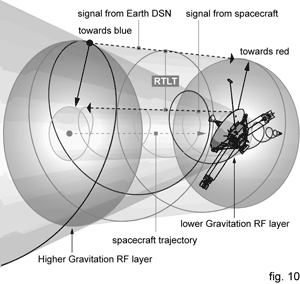
At one point, the blue shifted frequency might become so high that it would disappear from Earth’s RF perception range. As a body of lower gravity than the Sun, seeing with Gamma rays Moon actually appears brighter. Correspondingly, the effect of travelling towards bigger gravity systems would be as we were accelerating and to observers on Earth we would appear more and more red shifted. At one moment the effect of acceleration would increase so much that it would make us disappear out of Earth perception range. The good illustration for that would be to imagine the scenario in which this acceleration gets even faster than Earth’s RF layer speed of light. Signal from the Earth would be catching something it would be impossible to catch. Accepted terminology for that scenario is a Black Hole. It is in accordance with a result of Pound-Rebka experiment; When the photons from the top of the tower were measured at the bottom, their wavelengths were slightly decreased (blue- shifted); and when photons from the bottom were measured at the top, their wavelengths were increased (red-shifted) by the same amount.
This phenomenon implies that measuring distances and physical events with our RF speed of light would give us different results for different gravity RF layers.
According to Einstein's General theory of relativity light bends as it passes near a massive body. Two British expeditions conclusively observed this effect during the solar eclipse of 1919, when the Sun was silhouetted against the Hyades star cluster, whose positions were well known.Although it was later shown that mistakes in calculations were as big as their result itself, their measurements of several of the stars in the cluster have shown that the light from these stars actually did bent as it grazed the Sun, by the exact amount of Einstein's predictions. That led to various explanations for variety of peculiar visual effects around intense gravitational fields such as Black Holes. It also implied that light cannot escape from Black Holes and that our space is curved (which is true, although we would be more precise if we used terms "contracted" and "extracted" instead of curved). Furthermore, the idea of light bending produced some interesting ideas such as light spinning around Black Holes. If light speed is supposed to be constant all those ideas are in severe contradiction to its nature. Being trapped certainly doesn't mean moving at a speed of 299.792.458 meters per second and in case of bending next to intense gravitational field, light would have to gain some extra speed caused by spin effect. If thise strange effects would be happening inside of a galaxy, it would be interesting to imagine how that picture of light making U-turns is supposed to look to an observer from neighbouring galaxy?
A very simple scenario to explain curved space phenomena is a thunder.
When the lightning strikes it produces very strong and clear sound. To reach us, that travels through different density air layers and therefore changes its speed. Closer to the Earth, the air is denser than higher above so the sound spreads faster. Air density might also get influenced by temperature, moisture, wind and various turbulences. Even if we neglect the bouncing effect, the sound of thunder we are going to hear would be a variation of different frequencies, starting from very high and moving towards lower ones. What we would actually hear would be a result of Doppler effect. In the case of light travelling through different gravity time layers, higher sounds would be red shifted and lower ones would be blue shifted. The picture of our night sky would be something like an eternal light thunder.
Let us now go back to what happened during the Sun eclipse, on May 29, 1919? The light from stars of Hyades cluster passing behind Sun appeared on its opposite side before expected (but still on time predicted by Einstein's calculations). The conclusion was that the star was still where it was suppose to be, but since the Sun’s gravity bended the light ray, it appeared on the opposite side even if it was still behind. That was the triumph of Einstein's theory known today as one of Three classical tests (fig. 11a).
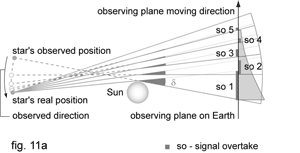
According to General relativity predictions, light bending is stronger when closer to the Sun and gets weaker with a distance. It means that, as the star – Sun distance increases the bending angle gets smaller. What we would actually see is the illusion of the star from the direction of the incoming ray (after it’s bent). In that scenario, following its appearance, star would start to move back towards the Sun, make a u-turn, and then, after light path straightens again, slowly continues to follow its predicted appearance path (fig. 11a).
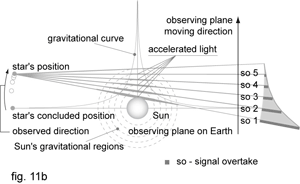
So the nature holds a different answer. Sun’s gravitational time dilation slows down the time and increases the meter unit. Light ray passing beside theSun changes its RF and its seconds get slightly longer. In one second of its time, light travelles longer way. Seeing from our RF layer, light was speeding up. The gravity time dilation and speed of light acceleration is more significant in region very close to the Sun and it is dropping down exponentially. That corresponds to Einstein’s prediction of light bend decrease when further away from sun. On May 29, 1919, British explorers saw the star appearing behind the Sun sooner than expected. It wasn't because of light bending. The same gravity lensing effect happened because the light ray, relative to our RF, travelled faster (fig.11b).
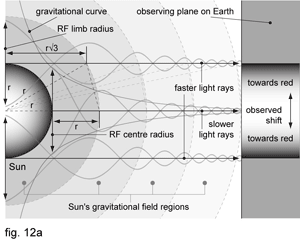
This consistently explains the observed centre to limb wavelength shifts variation anomaly. Let us consider the surface of our Sun. When observing its photosphere, it appears more red shifted at its limb than at the centre of the disk. When light from its centre reaches the Earth, it actually travels a shorter way through Sun’s gravitational field. Counted for time dilation and light speed acceleration, it travels slower than when coming from the limb when travels tangentially above the surface. Therefore, the difference between our speed of light and the one near the limb gets greater, which results with in a larger red shift (fig. 12a)
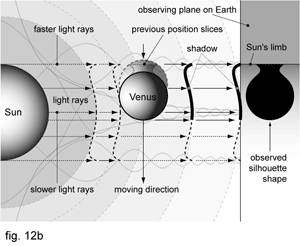
The same physical principle is responsible for Black Drop effect observed by transition of planets when on Sun’s limb. Since the Sun is not a disc but a sphere, light from its limb reaches the silhouetted planet and the Earth slightly later than light from its centre, because the way light ray has to travel is longer for Sun’s radius. Considering that transiting planet is moving, it makes the contour of transiting planet little bit distorted. As if we made the inverse process of projecting marbles shadow on the edge of the ball. But since the light coming from the limb travels longer way through Sun’s gravitational field it means that it is slightly faster. So the delayed signal from the limb gets slightly overtaken, which makes the picture appear like the part of it is being repeated (fig. 12b).
Some other good examples that illustrate errors between measuring events in different RFs with our RF speed of light are 0,43" arc second of advance of Mercury's perihelion and Pioneers anomaly.
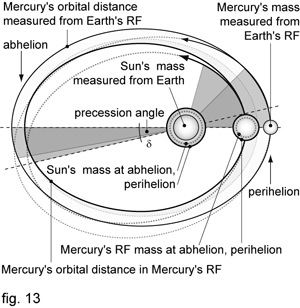
As celestial object whose orbit is closer to Sun than Earth’s, Mercury's RF layer is slightly dilated. What we calculate is a behaviour of space body in its orbital RF layer so we don't take into account a clock on Mercury (what Einstein did), whose gravity and speed would add up to its time dilation (that would certainly have to be considered if we would do our measurements from there). So, according to Swartzchild formula for gravitational time dilatation, one second on Earth counts about 1,00000001487 in Mercury's orbit RF layer, which means that in one Earth's year time Mercury gains about 0,47 seconds. An extra time to be considered when using
Another example of wrong measuring caused by using our RF layer constant speed of light that we mentioned above is Pioneer's anomaly which has been known as Pioneer's mystery for almost twenty years. For about 30 years, as they've made their ways to the edge of the Solar system, the two Pioneer spacecrafts (10 and 11) were tracked with enormous accuracy - to one part in a trillion. After scientists analyzed the tracking data with the most sophisticated statistical and computer algorithms, taking into account all the known forces that can affect these spacecrafts, there was still a deviation from Pioneer’s predicted motion.
Both spacecrafts were slightly blue shifted and their position in space didn't match to where they were supposed to be. They seemed to be slowing down for about 8000 miles per year from their predicted motion. It isn't much if one considers their travelling speed of about 12200 m per second. But in the last thirty years it accumulated to a distance almost equivalent to that from Earth to Moon. Scientists have being forced to consider the unthinkable: something may have been wrong with their understanding of The Laws of Physics. NASA's Jet Propulsion Laboratory scientists have been searching for an explanation since 1980. But as of yet, they have found nothing conclusive.
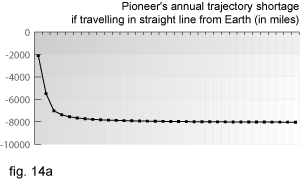
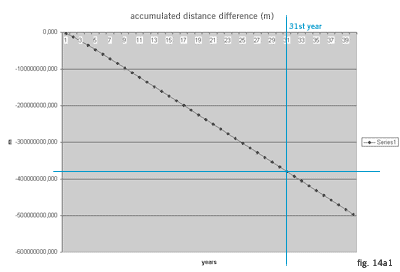
Being twice as far from Sun as Pluto, Pioneer 10 is travelling further and further from Sun’s gravity influence (which is 99% of solar systems mass). We use Schwarzchild formula to calculate gravitational time dilation for each annual travel region. Each region is 384.739.200.000 meters which is the distance Pioneer should travel in one Earth’s year time. We convert that distance in light seconds (the time it takes light to travel that distance) which is 1.283,351831352600000 seconds. Calculating Pioneers speed and direction we will take its predicted position for 33rd year of travel. Converting that position in light seconds one comes up with 39.783,906771930600000 seconds which makes about 11,051 hours. If the speed of light is considered to be constant, that would be the travelling time for our signal to make one way contact with the spacecraft. Since signal is travelling through different RF layers, when dilations from different travelling regions are counted together, predicted time for signal travel would be dilated to 39.783,906278418500000 seconds. To get a value for annual negative acceleration we should first subtract dilated with non dilated signal. The result, -0,000493512052344 seconds, is the time for which expected signal was overtaken in one way communication. Since for determining spacecraft's position in space RTLT is used (Round trip light time, which is in fact definition offered from Einstein for clock synchronization by light signals), we multiply it by two (the signal should travel there and back). We subtract the result (- 0,000987024104688 s) with the number we got by using the same procedure of calculation for previous year which is in our case - 0,000953438138822 s (and we are interested in annual data). This result of negative time is multiplied with the distance Pioneer should travel in one year time (384.739.200.000 m). The result is the Pioneer's annual trajectory shortage and equals - 12.921.837,6385979 meters (- 8.029,24160087789 miles) (fig. 14a). When we make a sum of these annual values the result for 31 year would be -379.746.864,417969 meters. Average distance between Earth an Moon is 384.400.000 meters (fig. 14a1).
To determine the exact distance of spacecraft in deep space measured with our RF speed of light, we end up with a simple equation;
![]()
where s is a distance expressed in our RF units, se is expected distance, td is dilated time, and 2 is for Round trip light time.
Since td=cd=sd, it is the same if we write;
![]()
or
![]()
From equations above, it is obvious that less intense gravitational fields would slow down the spacecraft, relatively to our RF, and vice versa.
What does this prove?
The Pioneer's RF accelerated and, to compensate for perception, its speed of light decreased proportionally. Because of that, the spacecraft time experience didn't change.
If we take velocity formula v=s/t and consider same value gravity driven meter (s) and second (t) contraction, velocity (v) for each RF, which is in our case c, wouldn’t change. But since the (t) and (s) unit values would differ from our RF, c unit would be different correspondingly.
Pioneer's distance from the Earth was measured by a signal travelling at, as considered wrong, the constant speed of light. While Pioneer's meter and second became shorter, the light seconds got shorter proportionally. In other words, in one second of our time, light travelled shorter way. Seeing from our RF layer, the light was slowing down. Because of travelling shorter way, the signal with a time code we sent to Pioneer came back a little bit to early. By calculating time it spend travelling, with Earth’s "physical constant" speed of light, and knowing its travelling speed, it is obvious that the result would lead to a conclusion that Pioneer is slowing down (fig. 14b). Pioneer’s tracking data is actually a function of its meter, time and light speed contraction driven by gravity.
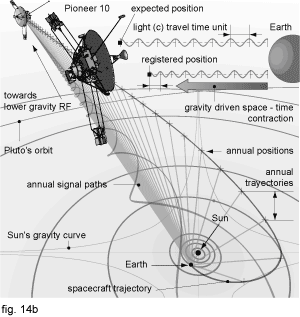
It also proves that light energy and speed, relatively to our RF, is decreasing with the decrease of gravitation. Correspondingly, it increases when closer to more intense gravitational fields. It corrects a mistake in General theory of relativity saying that the energy of light is falling down while trying to leave gravitational source. That presumption led to a wrong interpretation of red shift phenomenon. The result was a domino effect which produced numerous of other misinterpretations.
Opposite to strong gravitational fields which would attract other bodies, the celestial objects in very low gravitational fields (including those blue shifted out of our perception range), relatively to our perception point, would act as a balloon (fig.15).
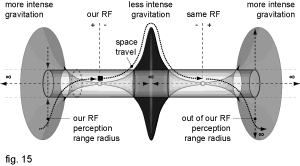
Because force of gravitation falls off whit a square of its distance its time dilation is changing correspondingly. This means that travelling to a certain planet from another star system, would be like climbing uphill with its top constantly getting away. Time would accelerate and the speed of light would slow down. Each day, approaching to the top, we would make lesser progress (climbers to
If the universe had its end and was expanding, all of the celestial bodies would start to experience the “uphill phenomenon” we mentioned before. The “uphill phenomenon” would increase towards the edge of universe, which would mean that those objects would actually have to be more blue shifted than others. It definitely doesn’t fit to observations, although the conclusion that the furthest objects observed should be the closest to the edge is very hard to understand. Somehow, it appears that we still put Earth in the centre, even unconsciously.
If we imagine a well known model with balls on a rubber plane, the less intense gravitational field balloons described before, would act like hills between their valleys. The hills would act like a balance to their attractions because they would have to climb them to get to each other. The required distance between objects would increase with their mass. But since their gravity would increase their second and meter unit, the perception of distance between them would correspondingly decrease. The heavier the balls, the bigger the hills between them. And the closer they are the steeper the hill angle (till certain distance, of course).Looking at that picture it looks quite obvious that small objects on the hills would have no other option but to and up in one of neighbourhing valleys. But if we imagine that the rubber plane is of infinite elastic they would also make their hills and valleys, and like the stones on mountains, more or less they would keep their place on different altitudes. Being closer to bigger objects, faster rotation would produce deeper valleys and correspondingly bigger hills. The same scenario would be found on the hills between them, so the process would repeat itself forever.
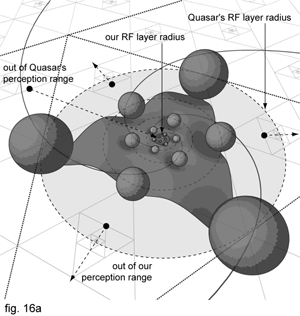
The geometry in fig. 16a is an illustration of such a balanced rubber plane module which can be repeated as a pattern or can grow in both directions forever (positive and negative). In both scenarios, it is obvious that the furthest objects for any RF would be the biggest, doesn’t matter from which position observed. The “balls on a rubber plane model” is a simple illustration which might explain the apparent lack of quasars at short distances.
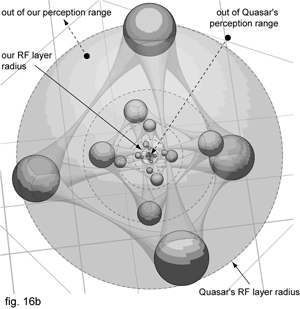
Figure 16b is the 3D tetrahedral version of the same model whose structural principle reminds of the atomic valence bond.
The more intense the gravitational systems are, the further they would appear to be. And the more red shifted they would be. So if we take galaxies as an example of very intense gravity systems, all of them would appear as they are moving away from us. This was the result of Edwin Hubble's observations who noticed that all of the galaxies, without exception, were red shifted. The furthest galaxies measured the biggest, and according to red shift interpretation their getting away speed appeared to be the greatest (Hubble's law). It happened to be one of the most important discoveries to prove the theory of expanding universe with the conclusion of Big Bang as its start. Consequently it led to the Big Crunch theory as one of possible scenarios for the end of our Universe. The last came as a conclusion after galaxies' red shifts observations. It appeared as theirs "acceleration" was decreasing.
One of the reasons for that might be that our RF layer is slowing down. The cause of this can be our galaxy arm mass growing influence. Our Solar system might be getting closer to
In both cases (either travelling towards lower or higher gravity systems) if difference between Earth’s and spacecraft trajectory gravity field would constantly increase (even if compensating for shifts) at a certain point of time, spacecraft would disappear out of its start point perception range. Nevertheless, it would still be there, in space. With the progress of technology which would allow us, on Earth, to capture signals from more dilated time, the spacecraft would suddenly appear again. At the same time, the Black Holes' radiuses would become smaller. We would be able to see some parts of space currently being hidden behind their "event horizons". Possibly, the collided particles in particle accelerator would appear shorter after collision. The back radiation image (WMAP) would show us some new secrets of space with low gravitation, faster time and slower light. Those seeking Dark Matter, might find a new physical proof of its existence.
Some of these "beyound limits" explorations might be performed if we launch our instruments in different gravity RF layers. Observing from a point closer to Sun would capture little bit of data behind Black Holes' "event horizons"... Suddenly, we might discover a whole new set of quasars and galaxies which are bigger and further than any of those giants we currently know about. The far clipping plane of the edge of our universe would slightly expand.