When the new game, chess, was presented to the emperor of China, he loved it so much that he offered the inventor anything he wished as a gift. At first, the emperor was impressed by the modesty of the inventor's request. He asked the emperor to put one grain of rice on the first chess field, two on second, four on third, and so on, continuing with exponential growth. When the rice grains were doubled thirty two times, which is half the number of squares on a chess board, there was still only about one acre worth of rice... to fill the entire chess board it would require 18,446,744,073,709,551,615 grains. If a grain of rice would be counted out every second, it would take 584 billion years to count them all. It is probably more rice then ever grown on the planet Earth. And what is sixty four chess fields compared to a billion? Or a Google? I don't know if the emperor lost his kingdom or the inventor lost his head.
To draw the curve of that magnificent growth, one should make an arc which is one fourth of a circle long. Its radius would be a side of a square with the value of 1. The next arc would continue where the first one ends, following its tangential direction. Its radius would be a side of a square which is a side of a previous square times two. And so on, repeating the same principle sixty four times... (fig.1).


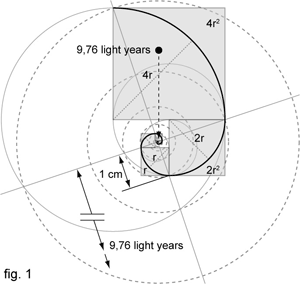
If the last point of the first arc is one centimetre away from imaginary centre of created spiral, the last point of sixty-fourth arc would be about 9,76 light years far! (Let us still count in light years.)