Let us now put a clock with its second hand in the imaginary centre of our spiral. Our second hand is going to be a light ray beginning at the sixty-fourth arc of negative, and ends in corresponding arc of positive exponential growth. It takes one second for hand to make a circle. The radius of a big circle is about 9,76 light years long. To close the circle in one second time, the end of our clock hand would have to move at a speed of about 579.521.556.646.170 km/s which is about 1.933.075.837 times faster than the speed of light. If we supposed that speed of light was the fastest speed our clock hand can manage, it would take about 61,3 years for its end to close the circle. At the same time, the other side of the clock second hand would move at speed of about 0,0000000000000000001 (1x10^-19) cm/s meaning (since if anything deserves approximation this does) it would actually stand still. But if we scale our world in no matter which growth direction, in both cases it would take one second to close a circle.
If we construct a Light second clock it would have a degree of 299.792.458 metres, exactly the orbit light travels in one second. We are going to call this orbit "our reference frame (RF) layer". If we then create an animation sweep of light ray moving at the constant speed in one direction, and at the same time making one second turns, the geometry we are going to get is a spiral shown in fig. 2a.
 

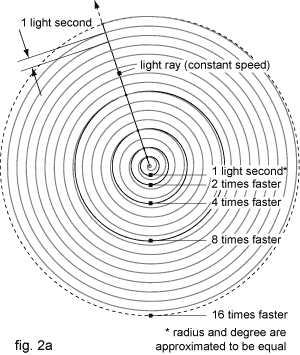
The problem arises after ray gets of our clock degree orbit because it would have to turn either faster or slower than it actually can because of our experience with speed of light. We suppose that our Light second clock travels the same speed, in no matter which degree orbit.
To make a correction we shall slow down the turnings which means that, when light ray reaches the degree that is two times bigger than our light second it would rotate two times slower. Therefore, it would take two seconds to make a turn. The same rule is applied to all subsequent degrees, doubling in size. This means that to close a circle at sixty-fourth degree, travelling at the speed of light, it would take about 292.471.208.677,5 years. In our RF that light ray would then rotate at a speed of about one millimetre per year which is 9.223.372.036.854.775.808 times slower than the speed of light.
If the degrees of our light clock are scaled down with the corresponding exponential growth, each next degree would cut the time for one turn in half. After the sixty-fourth round it would turn so fast that our RF clock, with a degree of 299.792.458 meters, would turn 9.223.372.036.854.775.808 times per second (i.e. times faster than speed of light).
Animation sweep of discussed operation would be a spiral shown in fig. 2b.


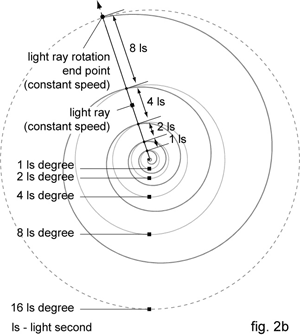
The idea of our Light second clock illustrated possible time gaps between different RFs. But each RF should experience the same time flow.
Imagine standing on a river bank. For this scenario a river would have no tributary. The riverbed width defins our RF and the speed of river stream corresponds to our light speed. Each time unit, a certain amount of water is flowing beside us. The amount of water is going to be our perception. If we changed our RF by moving upstream, the river would become narrower but our perception would stay the same since there would be the same amount of water flowing beside us. It is because river would flow faster. Correspondingly, if we changed our RF by moving downstream, river bed would widen and its flow speed would decrease. Looking from our first RF position, the narrower part would be a slower RF with faster light. Following the same logic, wider part would be a faster RF with slower light. But if we measure the speed of light, moving up or down, we would always get the same result. It is because wherever on the river bank we move, our time perception would stay the same. There would always be the same amount of water flowing beside us.
So we would be convinced that speed of light is an unchangeable constant.
Suppose we got a phone call from our friend living some distance upstream. We both "know" that our river flows the same speed, doesn't matter where. So we decide to make a little physics experiment by measuring river length. After our clocks are adjusted, our friend sends us a little paper boat, with the launch time written on it. After some time, the paper boat appears and is picked up. We compare current time on our clock with the time written on it. All we have to do is calculate its travelling time with speed of our river. And then call our friend. The physics experiment finishes "successfully", and now we both "know" the length of the river bank between us.
It is obvious that our calculation was wrong. And as the difference between riverbeds widens, and actual river length between us gets greater, the error in our calculation increases. (The question is, of course, whether in real world communication with our friend from very different RF layer would be possible)