
Time and free fall
Free fall starts with infinite slow speed.
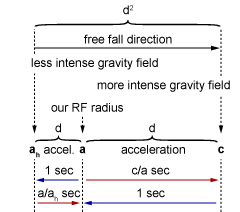
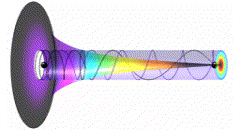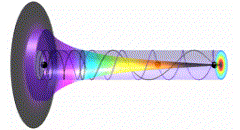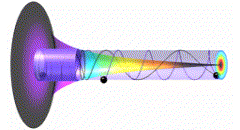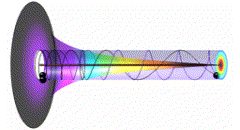
In an infinite small fraction of time falling body makes infinite small distance. As our dilatational snapshot defines our time, those infinite short distances and time intervals are in fact out of our space-time perception horizon. This speed increase from infinite slow to infinite fast, changes the falling object space stretchiness. So the free fall can be presented through a spectrum (fig.01).
 |
 |
 |
|
fig. 01
|
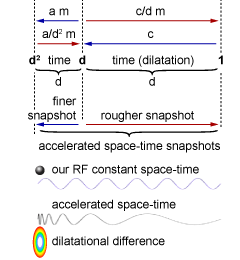
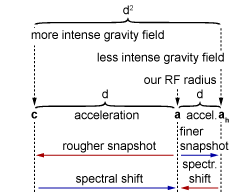
Shortening dilatation, in other words decreasing gravitation (compressing space-time), measured light speed stays unchanged. It means that in ten times smaller gravitational fields, measured light speed value is in fact ten times slower than ours. If we compare it to camera, it is as exposition (gravitation) decreases time snapshot (dilatation) but since filmed speed (speed of light) decreases as well, the length of captured frame stays the same.
Continuing that process, we capture smaller and smaller amount of space-time. In other words we perceive finer and finer details of space-time fraction. Our perception reminds the same, but compared to RF we left, our time accelerates and space gets more and more compressed.
So, in a free fall, those infinite small fractions of space-time get more and more significant.
We take our nested acceleration “na” as a starting RF free fall space-time fraction
![]()
which is about 0,0000000327 meters ( “da” stands for acceleration dilatation). Compared to our RF acceleration, it differ in dilatation, which means - time.
![]()
In other words, nested acceleration RF second lasts our dilatation. Each second of their, and dilatation of our time, speed increases for 0,0000000327 meters (na) of our space. If acceleration stays the same, counting from that RF, it would take a/na time to reach speed of our velocity at first second of a free fall. Counting in their units, it would amount some 30.538.327 seconds. For us, it would last only a second… In fact, in one second of our time, and 30.538.327 seconds of their time, nested acceleration RF reach its speed of light which is our acceleration. So nested acceleration became our acceleration.
Each next second of their time, speed continues to increase for “na” amount. Since our nested acceleration accelerates for its nested acceleration “2na”, “na” amount increases as well. In a second of our time, “2na” accelerates to “na”. So the next second “n”, speed “v” of a free fall increases twice;
![]()
while speed increase, meaning acceleration, stays the same;
![]()
(Approximately, since each nested acceleration has its nested acceleration where each transforms into a higher acceleration nest. And those acceleration nests are infinite…).
On a bigger scale, in our RF, this nested acceleration is added to acceleration, and each is multiplied with time (in seconds) of a free fall.
![]()
In our space-time perception, acceleration nests are so insignificant that we round our free fall speed increase to 9,807 meters per second.
If that acceleration stays the same it would take us 30.538.327 seconds to reach speed of light. At that point, our acceleration would be 299.792.458 meters per second, and 9,807 meters per dilatational fraction of time. Light speed became acceleration and acceleration became nested acceleration. They relate so as nested acceleration relates to acceleration;
![]()
The difference between nested acceleration, and light speed acceleration frame of reference is power of time;
![]()
This power of time is the range of our perception (fig.01).
Considering our nested acceleration increase which transformed into our acceleration, our speed increases twice (approximately, because of other nested acceleration levels). The advance of speed, as in scenario above, stays the same. It means that each next second “n” of light speed – acceleration RF, Light speed and its dilatation, which is our gravitation, increase for their amount;
![]()
To get distance we traveled through to reach speed of light, expressed in our units, we start with formula;
![]()
where “s” is way traveled, “a” is acceleration and “n” stands for time of a free fall (in seconds).
Since we now that time, which is reached speed (c) divided by speed advance per second (a), that formula is modified to;
![]()
Having in mind that nested acceleration accelerates as well, moreover it transforms to acceleration, given amount should be multiplied with that acceleration stretch factor;
![]()
So, the formula for distance, we have to fall over to reach speed of light, would be;
![]()
It amounts around 9.155.160.787.158.480 meters…
Calculating from Light speed RF with corresponding space-time units, given amount should differ for dilatation (since those RF’s differ in time).
![]()
The result is speed of light enlarged for two accelerations. Looking from their RF, nested acceleration (our acceleration) stretched for its amount.
![]()
So the next second of their time, speed of a free fall (speed of light) increases approximately twice;
![]()
while speed increase stays the same;
![]()
Calculating from Light speed RF, complicated formula for distance traveled from our RF to reach speed of light can be simplified to;
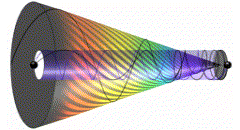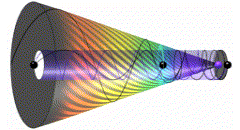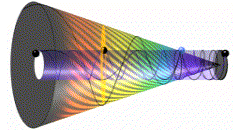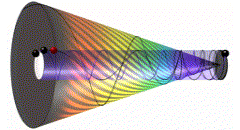
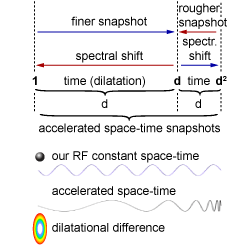
Making space-time snapshot finer, occurrence of tiny frequencies decreases, which relatively results with increase of their wave time. From black, they appear in blue. Decreasing further, they move towards red. Red frequencies disappear, and new appear from blue. So the spectrum we perceive stays the same (fig. 02).
 |
 |
 |
|
fig. 02
|
When first scientific satellites unexpectedly discover radiation belt in Earth’s magnetosphere, one of the scientists working on its explanation exclaimed: “My Good, Space is radioactive!”.
In fact, the appearance of space fraction, i.e. its tiny frequencies, which were unperceivable from Earth became visible from place of smaller gravitation and dilatation which means shorter snapshot.
For our refined snapshot perception, frequencies decrease, so our perceivable spectrum descends more and more towards blue… (fig.02)
Subatomic particles increase in size and their orbital velocities slow down. Further refining snapshot, we might land on an electron which orbits around some 8,5 light minutes distanced nucleus. Time and space decreased so extremely, that orbital period of our electron counts 365 our new days. Other nucleuses are light years distanced from us. The snapshot is so short that they look as they don’t move.
Fussy surface of an electron looks as it is frizzed in time. There are mountains and valleys around us…
Further shortening our space-time snapshot, we continue our perception refinement. The subatomic structure of an electron we landed on becomes our perceivable universe. Particles are huge and distanced stars. Our space-time snapshot became infinitely short so we see them as they stand still. We might land on one of its particles and enjoy its beautiful hilly surface frizzed in time. Further pressing our space-time, particles structure becomes universe…
If we increase our acceleration, the snapshot becomes longer. Since their occurrence in longer snapshot gets bigger, the flat line signals becomes red. Soon, we start to perceive black holes and unknown giant distanced galaxies and quasars. The space we left disappears in blue. Our snapshot lasts so long that each second of our new time, captures thousands of orbital cycles of a planet from which we started our journey. Its sun gets more and more blue shifted and disappears in black. The universe we knew is lost somewhere between billions of particles of our new space-time world…