Universal principle of orbits

From equivalence principle of relations between gravitations and corresponding dilations

comes forth that relative elliptical trajectories are in fact absolute circles.
Relation between periapsis “P” and apoapsis “A” equals to relation of their dilations.
Periapsis multiplied with its orbital dilation “d_P” is equal to apoapsis multiplied with its orbital dilation “d_A”.

Since

comes forth that periapsis multiplied with its corresponding orbital gravitation “g_P” equals to apoapsis multiplied with its orbital gravitation “g_A”.

That relation is the same for all of the orbits of observed system which dilation is determined by its rotational centre gravitation.

("_M", "_V", "_E" stands for Mercury, Venus, and Earth)

For different orbital systems, those orbital constants relate to each other as their rotation centre relative masses calculated from our RF.

From gravitational equation expressed through orbital velocity and light speed

we derive formula for orbital velocity which equals to square root of gravitational and light speed product

From a principle that the speed of light equals to orbital gravitation divided by its orbital dilation, follows the equivalence applied to orbital velocity divided by corresponding orbital dilation square root;

and the analogue equation for orbital velocity which equals to corresponding gravitation divided by square root of dilation;

It comes forth that the square root of gravitational dilation is a time fraction in which light moves over orbital velocity space fraction amount, and in which orbital velocity moves over gravitational space fraction amount.

In accordance to the equations above, follows that the orbital velocity equals to light speed multiplied with square root of corresponding orbital dilation;

Analogously to previous, gravitation equals to a product of orbital velocity and its corresponding dilation square root;

If orbital velocity is calculated in universal space time variables “v_ou”, rather then in meters and seconds, to get amount expressed in gravitational space fractions we divide it with corresponding orbital gravitation value. To get result for corresponding dilatational time fraction we further multiply it with its orbital dilatation

The power of that result equals to orbital dilatation;

From there and from relations above, the orbital gravitational dilatation is calculated. It is equivalent to a power of orbital velocity divided by a power of light speed as well as a power of corresponding gravitation divided by a power of orbital velocity;

From equations above, we write the equivalence;

Derive from there, we have that speed of light equals to a power of orbital velocity divided by corresponding orbital gravitation;

Since

and

consequently, we write the equivalence;

Therefore, gravitation relates to its corresponding orbital velocity so as orbital velocity relates to speed of light. Those relations are equivalent to a square root of corresponding dilatation.
If we expand the sequence of numerator-nominator order (gg, vv, cc), we end up with;

which illustrates the infinity and regularity of pattern.

From previous equations for orbital velocity, equations for escape velocity “v_esc” are derived;

and

We conclude that the dilation, as a consequence of orbital velocity “d_v”, equals to a power of gravitation divided by two powers of orbital velocity as well as a power of orbital velocity divided by two powers of speed of light;

and

Furthermore, it implies;

and

where d_v stands for dilation as a consequence of orbital velocity.

From there we have the equivalence;

We conclude that two dilations as a consequence of orbital velocity equals to one orbital gravitational dilation;

Therefore, we have the equivalence;

From the universal principle of orbits which describes the equivalence between periapsis – apoapsis and their corresponding dilations, emerges that the product of orbital radius “r” with its corresponding dilation equals to the same product for any other orbit of observed orbital system with common centre of rotation.

It implies the same equivalence relation for orbital circumferences and their corresponding orbital dilatations

From there, it implies that the relation between orbital circumferences “o” equals to relation of radiuses and reciprocal relation of gravitations, square root of accelerations, dilations and speeds of light difference;

Further more, since orbital velocity equals to a product of light speed and square root of dilatation,

means that orbital velocity of particular orbit relates to another orbital velocity of same orbital system as the square root difference of their corresponding orbital dilatations.

If orbital velocity is calculated in dilatational fraction of time rather then in seconds we divide it with second - dilatational difference;

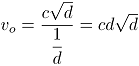
which is equivalent to

Moreover, orbital periods “p” relation equals to a product of orbital circumferences relation with its square root and to a product of orbital radiuses relation with its square root. Follows that the same equivalence applies for reciprocal relations between orbital gravitations, square root of accelerations, dilatations, and light speeds difference as well as to a half value of the same relation for orbital and escape velocities;

                           

From equivalence principle between radiuses and corresponding gravitations

and if “r₁” and “r2” are considered as celestial body and light second radius, “g₂” and “g₁” stand for corresponding gravitations. In that case “g₂” would be gravitation of one light second space fraction, and “g₁” would be gravitation in acceleration space fraction at celestial body surface, denoted as acceleration.

From that principle it comes forth that radius of celestial body for which measuring is performed, relates to speed of light so as its gravitation relates to its acceleration.

Follows that acceleration relates to speed of light so as gravitation relates to radius. Those relations are equivalent to acceleration dilatation in acceleration space fraction on celestial body surface;

Since acceleration is the value for which speed of light stretches in accelerational space fraction, follows that gravitation describes the stretch of celestial body radius which consequence is creation of its time.

From that equation, we derive that the radius equals to a power of light speed and dilation product divided by acceleration;

Which is if expressed with Newton’s gravitational variable “G”

Further, it is equivalent to gravitation uppon acceleration dilatation;

It follows that the radius equals to a square of orbital velocity divided by acceleration;

We derive the following equations for acceleration, speed of light, gravitation, and for gravitational and acceleration dilatation;

According to equation for radius explained through orbital velocity given above, results the equation for diameter “R” which is equal to a power of escape velocity divided by acceleration;

Conclusively, escape velocity equals to a square root of diameter and acceleration product;