
Forces
When describing forces we describe the space-time occurrence.
So the field we observe is frequency.
Imagine a thin rubber thread which one side is firmly fixed so that the other side can be stretched. The thread is let’s say 10 meters long. We stretch it pretty easy. For each next stretch we fold it in half so the number of threads are doubled and the length is shorten twice. Thus, the amount of thread, in other words its space, stays the same. When we fold it ones, there would be two threads and the fixing spot would be 5 meters away. Although two times thicker, it would be quite hard to notice that it is actually two times harder to stretch it.
Considering space-time as a vector product of time and speed, each time when we fold it again, what we do, we actually increase its occurrence in our space-time (fig. 01).
 |
 |
 |
|
fig. 01
|
After folding it five times there would be 32 threads and the fix point would be about 31 centimetre away.
If we succeed in folding threads 25 times, which is in convenient situation impossible, there would be 8 388 608 threads and their folded length would amount about 0,00000119 meters. Folding and stretching process have suddenly became extremely hard…
Now, lets say that our mass equals to mass of a thread so we would think of a force as a velocity.
To stretch tread we would have to accelerate its end at certain speed which would be equivalent to resisting force of thread but opposite direction. Lets say that, when thread is unfolded, our acceleration needed to stretch it for 1 meter, equals to 1 meter per second. Follows that we stretch it for one tenth part of its length. When thread is folded five times, we need to accelerate 32 meters per second to stretch it for tenth part of its length which is 3,1 centimetre… So in this scenario, number of threads would be our proxy to measure acceleration.
Unfolded length presents threads amount of space which stays constant, and folded length stands for its wave length (wave time), which is dilatation.
Further folding it, we decrease its dilatation and increase frequency so the appearance of rubber thread space-time in our space-time gets greater.
After folding thread between 28 and 29 times, its folded length (dilatation) equals to Earth’s surface dilatation and the number of its threads (acceleration) is speed of light. It means that force needed to stretch our folded rubber thread for 0,00000000327 meters, have to be equivalent to as we accelerate at speed of light…
If rubber thread would be folded 64 times, compared to scenario above, change of its length would be unperceivable and therefore insignificant. In fact, being 0,000000000000000000542 meters long it would be 60.405.221.040 times thinner, and the acceleration needed to stretch it for unthinkably small tenth part of its length would be 60.405.221.040 faster than speed of light!
Required energy to stretch rubber can be presented as spectral scale of its folded lengths i.e. dilatations (fig. 01).
If we think of a rubber as a space and instead of folding, press it to the size of an atom, we described nuclear force. Insignificant at big distances it immensely increases at extremely small distances unperceivable for our perception.
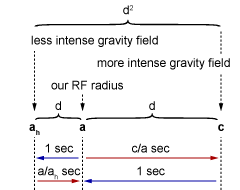
To stretch one light second space (299.792.458 m) for amount of our terrestrial acceleration (9,807m), we would have to accelerate at that rate. So that space would be dilated for a/c amount which is equal to dilatation.
![]()
When we “fold” that space between 24 an 25 times we arrive to length value which is the same as our acceleration space fraction (9,807 m). The speed required to stretch that space for relatively the same amount “ah”
![]()
is speed of light (table 01).
|
number of folds
|
folded space
|
space to stretch
|
required velocity (force)
|
| 0 | 299.792.458,000 | 9,816924666 | 9,817 |
| 1 | 149.896.229,000 | 4,908462333 | 19,634 |
| 2 | 74.948.114,500 | 2,454231166 | 39,268 |
| 3 | 37.474.057,250 | 1,227115583 | 78,535 |
| 4 | 18.737.028,625 | 0,613557791 | 157,071 |
| 5 | 9.368.514,313 | 0,306778895 | 314,142 |
| 6 | 4.684.257,156 | 0,153389447 | 628,283 |
| 7 | 2.342.128,578 | 0,076694723 | 1.256,566 |
| 8 | 1.171.064,289 | 0,038347361 | 2.513,133 |
| 9 | 585.532,145 | 0,019173680 | 5.026,265 |
| 10 | 292.766,072 | 0,009586840 | 10.052,531 |
| 11 | 146.383,036 | 0,004793420 | 20.105,062 |
| 12 | 73.191,518 | 0,002396710 | 40.210,123 |
| 13 | 36.595,759 | 0,001198355 | 80.420,247 |
| 14 | 18.297,880 | 0,000599177 | 160.840,494 |
| 15 | 9.148,940 | 0,000299588 | 321.680,987 |
| 16 | 4.574,470 | 0,000149794 | 643.361,975 |
| 17 | 2.287,235 | 0,000074897 | 1.286.723,950 |
| 18 | 1.143,617 | 0,000037448 | 2.573.447,900 |
| 19 | 571,809 | 0,000018724 | 5.146.895,800 |
| 20 | 285,904 | 0,000009362 | 10.293.791,599 |
| 21 | 142,952 | 0,000004681 | 20.587.583,199 |
| 22 | 71,476 | 0,000002340 | 41.175.166,398 |
| 23 | 35,738 | 0,000001170 | 82.350.332,795 |
| 24 | 17,869 | 0,000000585 | 164.700.665,590 |
| 25 | 8,935 | 0,000000292 | 329.401.331,180 |
| table 01 |
”ah” is the amount for which acceleration (and speed of light) changes in acceleration space fraction. The same as speed of light increases for acceleration in light second space fraction.
![]()
In other words, as discussed in “Explanation of Pound-Rebka experiment results”, ”ah” is in fact acceleration of acceleration.
Since “ah” has its acceleration and that acceleration accelerates as well, this process is infinite in both directions. In other words, for RF’s of bigger space and slower time, our speed of light is their “ah” value... and their relation to their RF's space-time speed is always dilatation (time). So those accelerations can be donated as “nested accelerations” with "n" as a symbol for nest number before or after a, depending on space-time direction. So we end up with infinite pattern of same relations;
![]()
where “1a” is “ah” value and “a1” is speed of light. We might say that “1a” is nested acceleration “na” of “a”, and “a” is nested acceleration of “c”. “c” is acceleration nest “an” of “a”. Again, we came to conclusion that acceleration and speed of light are the same. They only differ in time.
This is how pattern of the universe
![]()
or
![]()
is repeated.
Due to immense amount of force which is extremely hard to achieve, it is very expensive to perform extreme stretching described above. This is actually what is performed in particle accelerators. In a giant underground tunnels, particles are accelerated close to light speed and then redirected to bombard nucleuses…
But to achieve forces (velocities) above light speed there is no even theoretical solution to produce them since, by definition of nowadays physics, nothing can move faster then light.
However, there is a theoretical solution of how to perform stretches which require forces (velocities) googol times bigger than speed of light. And to perform those unthinkable hard stretches, the only force required would be the same force we needed to make a first, unfolded stretch…
”Give me a fixed point in space and lever long enough and I will lift up the Earth!”. Those where the words of Archimedes.
Imagine a lever which longer part equals to one light second (299.792.458m) and shorter is our Earth’s surface gravity amount (9,807m). Being at the longer end, we don’t need immense amount of force which means we don’t have to accelerate at speed of light to stretch our “folded” space for ”ah” amount. Instead, we only perform a free fall.
It is a pure lever principle. ”ah” relates to acceleration so as acceleration relates to speed of light. And their relation is dilatation (time).
It is because in both cases, light traveled the acceleration fraction of space in dilatational fraction of time. So space-time at lever ends differ for power of their dilatations (fig. 01).
Theoretically with a fixed point in space and lever long enough we can not only lift up the Earth, but brake an atom, stretch space and create time…