
Gravitation as a measure of space time stretching
The space around Sun is divided in light seconds “ls” space fraction markers (299792458 m). To measure acceleration “a” for each space fraction between markers the
![]()
"G" is Gravitational constant, "M" represents mass and "d" stands for distance.
For first ten light seconds, starting from Sun’s surface, the following values are obtained:
Table 1.
|
ls
|
distance (m)
|
acceleration (m/s2)
|
|
0
|
696000000
|
273,964
|
|
1
|
995792458
|
133,837
|
|
2
|
1295584916
|
79,064
|
|
3
|
1595377374
|
52,141
|
|
4
|
1895169832
|
36,950
|
|
5
|
2194962290
|
27,546
|
|
6
|
2494754748
|
21,323
|
|
7
|
2794547206
|
16,994
|
|
8
|
3094339664
|
13,860
|
|
9
|
3394132122
|
11,520
|
To calculate dilatational amount for each space fraction the Schwarcshild’s equation for gravitational dilation “gD” is used:
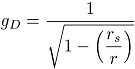
The “1” in numerator represents no dilated time, “r” is a radius and “rs” is Schwarcshild’s radius expressed with formula:
![]()
where c stands for speed of light.
Each space marker distance is treated as a radius at which light speed is multiplied with corresponding dilatational amount:
Table 2.
|
ls
|
distance (m)
|
gD
|
cd
|
|
0
|
696000000
|
1,000002121599437
|
299793094,03951
|
|
1
|
995792458
|
1,000001482871036
|
299792902,55355
|
|
2
|
1295584916
|
1,000001139740835
|
299792799,68570
|
|
3
|
1595377374
|
1,000000925568197
|
299792735,47836
|
|
4
|
1895169832
|
1,000000779154569
|
299792691,58466
|
|
5
|
2194962290
|
1,000000672735930
|
299792659,68115
|
|
6
|
2494754748
|
1,000000591893781
|
299792635,44529
|
|
7
|
2794547206
|
1,000000528396756
|
299792616,40936
|
|
8
|
3094339664
|
1,000000477203451
|
299792601,06199
|
|
9
|
3394132122
|
1,000000435053621
|
299792588,42579
|
Given light speed values represent relative light speed change in relation to our reference frame “RF” speed of light. Those values are the illustration of space-time stretching. Since longer second increases the space for the same amount (dilation of space equals to dilation of time), the Light speed result, measured from each particular space marker RF, stays unchanged.
The relative light speeds values are subtracted where given amount represent difference in light trajectory amount between markers:
Table 3.
|
ls
|
distance (m)
|
relative light speed difference (m)
|
|
0
|
696000000
|
|
|
1
|
995792458
|
191,48595
|
|
2
|
1295584916
|
102,86784
|
|
3
|
1595377374
|
64,20734
|
|
4
|
1895169832
|
43,89370
|
|
5
|
2194962290
|
31,90350
|
|
6
|
2494754748
|
24,23586
|
|
7
|
2794547206
|
19,03592
|
|
8
|
3094339664
|
15,34736
|
|
9
|
3394132122
|
12,63620
|
For acceleration results given in Table 1 the average values are derived
Table 4.
|
ls
|
distance (m)
|
average acceleration value
|
|
0
|
696000000
|
|
|
1
|
995792458
|
203,90052
|
|
2
|
1295584916
|
106,45050
|
|
3
|
1595377374
|
65,603078
|
|
4
|
1895169832
|
44,545969
|
|
5
|
2194962290
|
32,248082
|
|
6
|
2494754748
|
24,434711
|
|
7
|
2794547206
|
19,158597
|
|
8
|
3094339664
|
15,427100
|
|
9
|
3394132122
|
12,69025
|
Since, if measuring with constant units for space and time, acceleration is not a linear function but falls down with the square of distance, the average acceleration values of consequent exponential curve between markers are calculated:
Table 5.
|
ls
|
distance (m)
|
precise average acceleration value
|
|
0
|
696000000
|
|
|
1
|
995792458
|
191,48595
|
|
2
|
1295584916
|
102,86784
|
|
3
|
1595377374
|
64,20734
|
|
4
|
1895169832
|
43,89370
|
|
5
|
2194962290
|
31,90350
|
|
6
|
2494754748
|
24,23586
|
|
7
|
2794547206
|
19,03592
|
|
8
|
3094339664
|
15,34736
|
|
9
|
3394132122
|
12,63620
|