Space-time curvature and measuring

As shown in explanation of Poun-Rebka experiment results, Pioneer’s anomaly solution and advance of precession of Mercury’s perihelion, different gravitational fields have different dilatation, which according to equation for light speed “c”;

where “g” is gravitation and “d” stands for dilatation, implies that, relatively to our frame of reference, more intense gravitational fields have faster, and less intense gravitational fields have slower speed of light. In other words, for one light second region space stretches for gravitational amount which results whit light speed increase for corresponding gravitational amount;

where “c_d” stands for dilated speed of light.
This is why light speed at the bottom of  22.5-meter-high Jefferson Tower on the Harvard campus where Pound-Rebka experiment took place, compared to light speed at its top, increased for “a_h1“ amount which was 0,000000736 meters. If Tower’s height “h” would equal to acceleration amount “a” (9,807m), light speed (and acceleration) increase would equal to subtraction of Pound-Rebka’s light speed increase and the Tower’s-gravitational space fraction difference.

The result for “a_h“ value would be about 0,000000321 meters.
This amount is derived from measured wave time (wave length) difference "Δλ" at the top, of the signal sent from the bottom which is equivalent to "Δλ" of the signal send from the bottom and measured at the top. So the “a_h“ value equals to a product of "Δλ" and speed of light;

which is analogous to equation for acceleration expressed through light speed and acceleration dilatation “d_a“;

Since “a” is the acceleration in one light second space-time fraction, implies that “a_h“ amount stands for acceleration of acceleration space-time fraction where "Δλ" is the corresponding fraction dilatation and it is equivalent to a power of acceleration dilatation;

According to “a_h“ - “a” analogy, and since dilatation equals to gravitation upon speed of light (and acceleration dilatation equals to acceleration upon light speed),

comes forth that acceleration dilatation equals to subtraction of “a_h“ value and corresponding acceleration;

Scenario described above shows that space-time difference between bottom and top of the tower equals to difference of their wave time "Δλ" with corresponding acceleration and light speed difference “a_h”.
It means that one meter “m” and one second “s” at the bottom is for dilatational amount greater than meter “m_d” and second “s_d” at the top.

It implies that distance measured from the bottom, which means from more intense gravitational field, give smaller amount when expressed in corresponding unit for measuring space. In other words, measured distance appear closer.
The same applies for measuring time of events. Since one second increases for corresponding dilatational amount measured events last shorter.

Gravitational-dilatational difference increase, enlarges described space-time curvature (fig. 01).

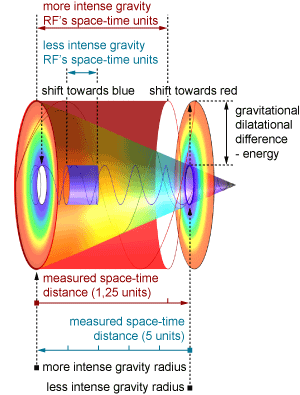fig. 01

Space-time curvature is actually the consequence of calculating physics with our constant speed of light. If that light speed difference (dilatational difference) is not included in measuring, the perihelion of Mercury advances more than expected, Pioneer 10 spacecraft unexplainably slows down and Galaxies don’t obey Kepler’s law of orbital motion.