methods

To calculate Pioneer's anomaly, two methods with the same principle were used. It was presumed that, while travelling through different gravitational regions, relatively to our RF, the signal second (t) and meter (s) units are changing. Since speed (v) is defined as v=s/t and in our scenario we are dealing with the speed of light (c), to preserve the same speed measured from each RF, it was concluded that, relatively to our RF, (c) should change for the same amount. To calculate that amount, Schwarzschild formula for gravitational time dilation was used.



R_s stands for Schwarzschild radius, R_o is radius, t_f is nondilated and t_o is dilated time.
For our case it was



where t_d is a symbol used for a time dilation, t_f equals 1, and R is a distance measured from the center of a celestial body (in our case the Sun and the Earth).
In both methods Sun's and Earth's gravity dilation were counted together. Although the Earth's gravity influence on greater distances is almost unnoticable, its amount is quite essential on its surface where the Deep Space Network (DSN) antennas are placed.

RTLT
For better understanding of how the spacecraft's position in deep space is determined, RTLT (Round Trip Light Time) is going to be described shortly. The method was offered by Einstein for clock synchronization.
Antenna on the Earth sends the signal with the universal time (UT) code targeting direction where the spacecraft is expected to be in time the signal reaches it. As soon as it arrives, it is sent back, pointing to where the Earth is supposed to cross paths with it (the signal from Pioneer traveles about 11,5 hours in one way communication). When the signal is received, its time code is subtracted from current universal Earth's time. That result is multiplied with a speed of light (which is considered to be constant). The received value is a distance light travels in two way communication. To get a spacecraft's distance from the Earth that value is divided by two.

first method
The first method, which is partially described in the article, approximates the Pioneer's real trajectory by assuming it moves in a straight line away from the Sun and the Earth. Its trajectory path exactly matches the signal path that was calculated to get the signal dilation accumulation amount. To compensate for the approximation, Earth's orbit was positioned slightly closer to Venus. This method is simpler because for each next year, values are just added to previous and it produces less numerical data. For this scenario the trajectory data isn't necessary, since the only Pioneer's value needed is its speed. Although the method is simple, it serves a purpose and proves the principle.
Knowing the spacecraft speed, its trajectory was divided in regions it is supposed to travel in one year time. This regions are then recalculated in light seconds. When calculating gravitational time dilation for each region, the distance values are used as Sun's and Earth's radiusis. Thise values are divided with dilation on Earth's surface value to get 1 for Earth's RF units.
The products of each region light seconds value and each region dilation value are counted together to get trajectory's light seconds dilation accumulation. This value is subtracted with non-dilated light seconds sum. The reslt represents light seconds shortage (signal seconds) advance for each annual travelling region. Since RTLT was used, this number was multiplied by two. To get the annual "slowing down" data, that result was subtracted with previous year result and multiplied by the expected annual region travelling distance (the product of spacecraft's speed and year's time).
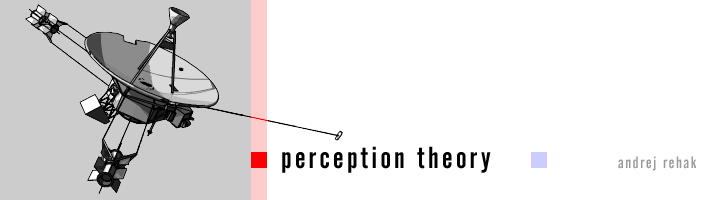
Although approximate, the result data almost exactly and fully explains the anomaly. It matches to spacecraft's oberved trajectory shortage (about 8000 miles per year) (fig. 14a0).

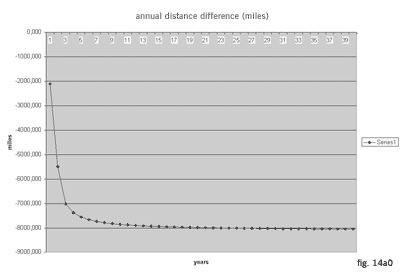
In about 30 years time, that difference accumulated to a value equivalent to a distance between the Earth and the Moon, which is averagely 384.400 km. This is allso consistent with our method calculation results (fig. 14a1)..


download the first method data sheet

second method
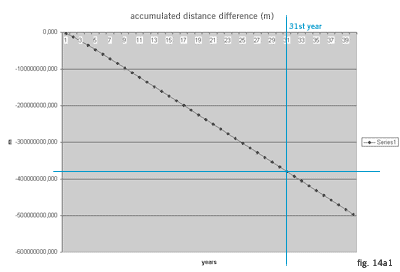
Second method uses the spacecraft's trajectory data. The Planets' Orbits from Alcyone software was used to import Pioneer's 10 trajectory data into Maya (fig. 01a).


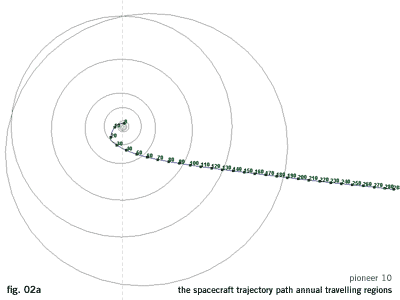
The spacecraft's trajectory path is divided in annual travelling regions (fig. 02a).

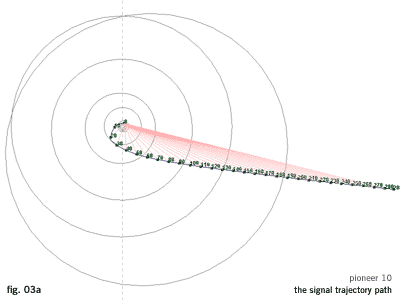
The signal trajectory path between each region path point and Earth are created (fig. 03a). To reduce the amount of numerical data, we approximate that Earth's position for each annual communication with the spacecraft was on the same point as on the day of its launch. Earth's rotation around the Sun would produce oscillations in the output graph, which is consistent to Pioneer's real data, but the main graph line would be the same.


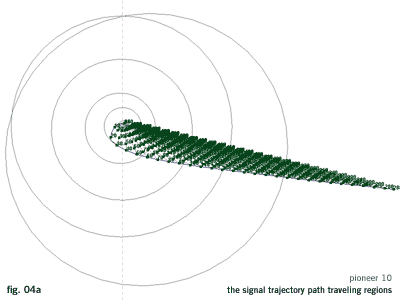
The paths are divided in annual timeline signal travelling regions (fig. 04a, 05a).


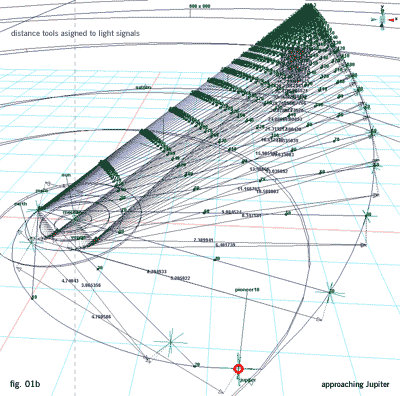
The locator point is assigned to each signal path and animated (moving from spacecraft's annual position point towards Earth). The animated locator point represents the signal on its path signal trajectory. For each signal point, two distance tools are created. One point of first distance tool is point constrained to Earth and another to animated signal locator point. The same applies to another distance tool which is point constrained to Sun instead of Earth (fig. 01b-04b)




download the second method 3D simulation
download the second method Maya file

For each year, the distance data (in AU) from Earth and Sun are gathered from all signal path markers output data and transferred to Microsoft Excel (to acquire the highest precision level, in the first version the xlPrecision plug-in was used. It was later abandoned since its data couldn't create graphs, and the sheets were meant to be downloaded, so for most Excel users the data wouldn't be useful)
This data was named the Expected signal trajectory points. It is converted to meters, and for each point the gravitational time dilation is calculated (for Sun and Earth). Each distance data from Earth is subtracted from the previous one to get a distance value of a signal path between marked points. It was named the Expected signal trajectory points distance, expressed in metres. Both dilations are counted together and divided with a value on Earth's surface (to get 1 for Earth's RF units). To get a signal trajectory dilation on a signal path between marked points (and not just dilation on marked points) the average value between points is calculated. It was named the Signal trajectory dilation. The expected signal trajectory points distance in metres is multiplied by a light speed value to get the expected signal trajectory points distance expressed in light seconds. This value is multiplied by a signal trajectory dilation value to get dilated signal trajectory points distance in light seconds. For each year the sum of the expected signal trajectory distance and dilated signal trajectory points distance is calculated separately. Each annual dilated signal trajectory distance sum is subtracted with annual expected signal trajectory distance sum to get annual signal trajectory difference expressed in light seconds. Because of RTLT, the result is multiplied by two and named the Annual signal trajectory difference RTLT, expressed in light seconds. The difference between those annual values (each year value subtracted from next year value) is multiplied by the annual expected signal trajectory distance in metres (sum of signal trajectory points distance for one year subtracted from sum of signal trajectory points distance of next year).
Although approximate, this result of annual signal trajectory shortage almost exactly and fully explaines the Pioneer's anomaly (fig. 14a2, 14a3). It is allso noticeable that the anomaly became significant when the spacecraft reached the Saturn orbit (which corresponds to received data).


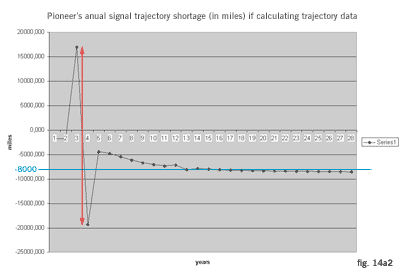
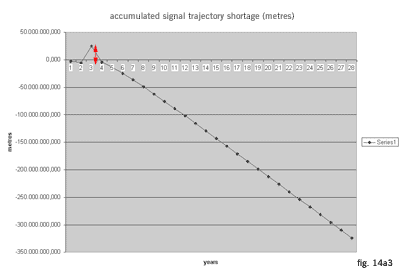
(The red marked jump in figures above occurs due to dilation differences while the signal was passing close to the Sun. When dividing signal trajectory path, the markers happen to be placed allmost at the same position as the Sun)

download the second method data sheet

Using both methods, the same result is achived whether calculating second, meter or speed of light contraction. Since t_d=c_d=s_d, it is the same if we write a formula for determining exact distance of the spacecraft in deep space: